Share
咱来谈谈范畴论
真正的无知不是知识的匮乏,而是拒绝获取知识;真正的理解也不是能懂得或者能造出晦涩难懂的知识,而是能把晦涩难懂的知识讲得通俗易懂。
当然即便很有可能不准确,聊胜于无,说这个话题的中文文章不多,最知名的比如阮老师的那篇 FP入门。
当然也可以去看看进阶版本的那个装逼指南。
当然数学爱好者可以去看看 抽象代数,我一朋友写的博客在这里。
这篇文章受限于作者的水平 也包括一些刻意设计 难度大概在阮老师和装逼指南版本之间,当然还是偏向阮老师那篇的。
这里我们讲的是纯范畴论,和函数式编程 关系不大,所以不要提什么纯函数、副作用、引用透明、惰性求值、高阶函数之类的。
范畴论(category theory)是什么呢…… 这个问题在提出来之前,肯定大家都得先膜拜一下那些Haskell大佬吧,可惜我不是,这真是一个悲伤的故事。
不过我今天不是来谈Haskell的,我一定不会用到数量过多的Haskell语法和概念,不过很有可能会曲解很多概念,毕竟其实我也不懂,只是为了大家装逼特意过来发福利而已。请大家放心,其实错了也不妨碍你们装逼的。
这篇文章假定你没有任何Haskell功底,也只会教你和入门范畴论基本理念相关的语法,入门请看这里。
历史上的东西,我们就不谈了,毕竟也比较好找,详情 wikipedia:Category theory。
一般的命名约定
- 对范畴论,
a b c都是对象、f g h都是箭头。 - 对Haskell,
a b c都是类型、x y z都是值、f g h同上。
含宏半群(Monoid)
范畴(Category)有两个组成成分:对象(Object)和箭头(Morphism, 态射)。
一个范畴其实也可以视作对象的集合,毕竟一般来讲箭头 f: (a -> b) 都是用于修饰对象,来描述另一个对象的,即便它也可以被用来做计算,毕竟函数式做计算都是 分支函数 和 递归。
下文中尤其注意要把 Haskell 的类型变量 a b 和范畴论的对象 a b 分开,不要认为 a b 和它们的类型有关……
当然集合也是分 有穷(finite)和 无穷 的,但给一个对象你都可以判断它是否属于某个集合。
Semigroup 就是满足这两个性质的 Category Set 集合:
- closure封闭律:
forall f g. exists h. h x = f (g x) - associative结合律:
forall f g h. (f.g).h = f.(g.h)其实是(.)closure运算的结合律
其中 (f.g) 就是表达一个 h where h x = f (g x)
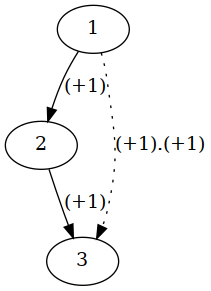
//ints.gv
digraph Ints {
one [label="1"];
two [label="2"];
three [label="3"];
one -> two -> three [label="(+1)"];
one -> three [label="(+1).(+1)", style=dotted];
}
dot -Tpng ints.gv -o ints.png
其中那两个 (+1) 从上往下分别叫 f, g;而 (+1).(+1) 是它们的 合成(composition),也是一个箭头,叫 h。(按一般约定会这么叫)
一般来讲为了理论的优雅性,大部分文章里 1, 2, 3 都被泛化为了 X, Y, Z(数学风格里单大写字母表示常量)。
这个 X, Y, Z 可能是人、花草、事物…… 以及一切范畴里的一切对象,只要它上面的箭头映射到同一个范畴(比如 人 的母亲是人、人 的父亲是人、事物 在物理上的最近邻仍是事物)就可以随便组合(比如,『你妈妈(f)的妈妈(g)』或者说『你的姥姥(h)』)。
至于那个结合律,一般认为是可以直接从定义导出的性质,当然前提是肯定等价,没有副作用。
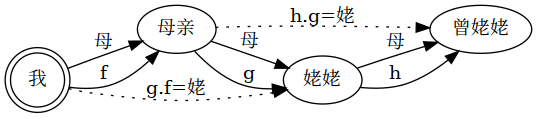
digraph Composition {
rankdir=LR;
me [label="我", shape=doublecircle];
ma [label="母亲"];
ma2 [label="姥姥"];
ma3 [label="曾姥姥"];
me -> ma -> ma2 -> ma3 [label="母"];
me -> ma [label="f"];
ma -> ma2 [label="g"];
me -> ma2 [label="g.f=姥", style=dotted];
ma2 -> ma3 [label="h"];
ma -> ma3 [label="h.g=姥", style=dotted];
}
嗯,「女老」就是姥姥嘛,我 的姥姥和 母亲 的姥姥都是 母 . 母,(f . g) . h = f . (g . h),就是说「姥姥的妈」和「妈的姥姥」一样。 怎么感觉有点奇奇怪怪的
Monoid 就是满足这个性质的 Semigroup:
- identity:
exists id. forall a. id a = a
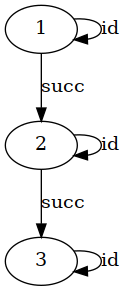
digraph Identity {
one [label="1"];
two [label="2"];
three [label="3"];
one -> one [label="id"];
two -> two [label="id"];
three -> three [label="id"];
one -> two -> three [label="succ"];
}
本节的最后我想告诉你,其实本文说的『范畴』都是指 Monoid 而不是我上面定义的 Category,那只是 directed graph有向图 而已。至于为什么我要出尔反尔,那是因为我从 五个人那里听到过五种不同的定义,我实在是有点迷糊了,搞不明白到底谁对谁错,以及范畴论到底是做甚么的,所以只好把 搞清楚 到底哪个是真正定义的 艰巨 任务交给读者们完成了。也是无所谓,一千个读者眼里有一千个哈姆雷特,你们开心就好。
Nat 是啥子
Nat 是自然数(natural number)的意思。
自然数的定义,一个是我们数学上那个『大家都明白』的简易模式识别版本(就是给正常人学的版本),我们知道上面可以进行四则运算,可是它和范畴有啥关系呢?
这里我们把自然数视为 0,或 另一个自然数+1,因为1是自然数的 基本单位,所有自然数均由1或0累积构成。
data Nat = Z {-Zero-}| S Nat {-Succeeder-}
succ = (S :: Nat -> Nat) -- plus one
succ :: Nat -> Nat
pred n@(S m1) = m1 -- minus one
pred :: Nat -> Nat
可是它和范畴有啥关系呢?
plus :: Nat -> Nat -> Nat -- (->) 是「右结合」的,这等价 Nat -> (Nat -> Nat)
plus Z n = n -- (n+0) = n
plus x n = plus (pred x) (succ n) -- (n+x) = (n+1)+(x-1)
虽然我们的抽象是这样的,定义也细致了很多,但它也是符合数学上自然数定义的。
(+)::a\to(a\to a)
Haskell 的中缀运算符是直接支持 (1+1)=2 这种模式匹配定义形式的,但是也有反括号 中缀式调用 一个函数:(0 `plus` 2) = (plus 2) 0
plus = \begin{cases}
0\to&id \begin{cases} 0\to{0}\\ 1\to{1} \\ \cdots\end{cases} \\
1\to&succ.id \begin{cases} 0\to{1}\\ 1\to{2} \\ \cdots\end{cases} \\
2\to&succ.(plus\quad 1) \begin{cases} 0\to{2}\\ 1\to{3} \\ \cdots\end{cases} \\
\cdots
\end{cases}
plus :: Nat -> (Nat -> Nat)
plus Z = id
plus x = ((plus . pred) x) . succ
嗯。函数(function) 是一种 映射关系(mapping),而不是一种 子程序(subroutine),这是数学函数、纯函数式编程。
不过呢 映射 是一种 单向关系,所以这么写的程序按上面那个梗(姥姥是妈妈的妈妈),给它「你的姥姥」是算不出「你」的,只能得到你的「妈妈的妈妈的妈妈的妈妈」也就是你的「太姥姥」,哈哈。
这里没有状态——不要当它存在、没有什么新不新旧不旧、放置和取出,就是一个个对象和不断映射它们的映射关系,分支函数实现「条件」、递归函数实现「循环」,权当你之前为了理解所作的变通,通通不存在。
模型本身并不很难理解,多琢磨一下几个小例子就了解了。
所以Haskell的 guard(分支)函数、case of、基于模式匹配定义的函数不是为了好看,而是它们本来就是那样而已。
所以Haskell的IO很难做不是为了实现惰性计算甚至线程安全,而是因为Haskell生来如此,设计就是纯的函数式编程。
Nat 的的箭头比如 (plus 1 :: Nat -> Nat),Nat 的对象就多了,Z、two = (succ (succ Z)) 都是。
然后你会发现怎么形式化语言的 terminal 和 non terminal 像是范畴里的对象和箭头呢?
那么如果有函数 (show :: Nat -> String) 呢?这就是要用到一个 更大的范畴 上的 箭头 (->) :: (* -> *),一个 Higher Kind类型种属,其中 * 是任一 Haskell 类型——Haskell 类型系统范畴 上的 对象,而这个大范畴视作集合,是所有 Haskell 类型的 并集类型(union type)。
比如,(->) 的那个范畴上就有一个箭头 id :: forall a. a -> a 和 (.) :: forall a b c. (b -> c) -> (a -> b) -> (a -> c),注意这里的 a, b, c 代表类型或者说 Haskell 类型系统范畴上的对象。
默认类型变量都是隐式声明的。显示写出 forall 也是可以的,不过需要开启 {-# LANGUAGE RankNTypes #-},这其实是一个类型系统上的语言特性(顺便也可以去看看 LANGUAGE GADTs,广义代数数据类型Generalized algebraic datatypes)。
class (k :: * -> *) => Category k where
id :: k a a
(.) :: k b c -> k a b -> k a c
type HaskType = (->) :: * -> *
instance Category HaskType where
id = id :: a -> a
(f . g) = \x -> f ((g x) :: b) {- a -> c -}
当然这样就产生了递归(准确的说是我们发现了,因为Haskell里始终就有……),就产生了许多许多更高维度(比如,对象是 (->))的范畴…… 这里都不讨论。
当然 (->) 并不是一个特殊的语法,它只是 Haskell Higher Kinds 的一个 类型构造器(type constructor) 而已,注意不是 数据构造器……
(->) :: TYPE q -> TYPE r -> *
那么此箭头在不在 Nat 范畴上呢?不在,因为我们知道任何 String 对象都不可能是 Nat 对象,它们之间不存在 实际上 的 交集intersection,而箭头 f: (a -> b) 里 a, b 需属同一范畴,所以这只能是 (String & Nat) 也就是(交集)* 上的箭头。
瞎想 Nat
想要有个基于 Nat 的 Int,就是有 符号 或者说正负的 Nat。
class Equiv t t' where
from :: t -> t'
to :: t' -> t
-- Int和Nat本不等价,教学目的,不准瞎复制。
instance Equiv Int Nat where
from i = if i >= 0 then (foldnl suc Z i) else undefined where
suc = (\n _ -> S n) -- flip (\_ -> S)
to Z = 0
to x = 1 + (to . pred) x
foldnl :: (b -> Int -> b) -> b -> (Int -> b)
foldnl f v = \n -> (foldl f v) [1..n]
首先可以有一个弱智一点的。
newtype BadInt' = BadInt' (Bool{-neg?-}, Nat)
instance Equiv Int BadInt' where
from i = (i < 0, from . abs i)
to (s, x) = let sign = (if s then negate else id) in
(sign . to) x
弱智不是因为它很直白,而是因为它的直白导致了存在 +0 和 -0 区分这种窘况……
为了保证 0 被良好区分开,我们认为要把负数和自然数(正数和零)的部分有一个划分。
forall n, x in Nat. n+(-x) < 0 => max(x)
来找到第一个绝对的加法负数因子 x=1,又因为 forall a b. a-b = a+(-b),而且 0-1 又被称为 minus 1/negative 1,所以
data Int' = P Nat | N1m Nat {- -1-x | -(1+x) -}
instance Equiv Int Int' where
from i = if i >= 0 then (P . from) i
else (N1m . from . abs . (subtract (-1))) i
to (P x) = to x
to (N1m x) = -(1 + to x)
Functor函子 们
class (Category c, Category d) => Functor c d t where
fmap :: c a b -> d (t a) (t b)
图是从 这里 盗 过来的,我懒得再画一遍了。
自函子(endofunctor)就是连接相同范畴的 functor。
type Endofunctor c t = Functor c c t
然后我曾经听到有人说『Monad单子 就是自函子范畴上的含宏半群』是什么鬼,大概意思应该是 Monad 是含宏半群上的 Functor 吧。
当然我是不了解的,据说 Monad:
- 是
Endofunctor t - 上面有
(eta :: a -> t a)(idc 到 T)、(mu :: t t a -> t a)(T T 到 T)
一般的用法就是 eta 拿来把一 (t a) 变成 (t t a) 然后 mu 弄回去,当然我是指不学术上的。
为什么它这么难呢?因为所有被构筑不是为了来解决实际问题的理论都是很难的,要不然你的智商余下一大把,体验不到挑战脑力的快感,也就使得这种理论事实上没有意义了。 虽然它们可能本来就很没有意义
所以为什么要有 Functor,模拟变量或者说『盒子』的解释也未必不可(虽然那只是很小一个用法而已)。
没有 (get :: Functor t -> t) 是因为要使这种函数有意义,就必须再配上一个 (set :: Functor t -> t -> Unit),不然『只能取』在惰性求值的Haskell里等价于 t 本身,Haskell从不是这样,自设计以来就不是。 虽然我好像也没有立场以这种语气说什么Haskell不Haskell
这个世界是无状态的,只由「对象描述(初始、或由态射组合而成的)」和「态射修饰」组成计算。 大家觉得Functor像盒子是因为它的确蕴存了『状态』,它「包住」了一个范畴,也就是某种可能的『取值』对象,理论上也可以说是所有的,只不过所有类似初始对象的东西都被箭头们修饰过了,根本没区别。
Functor 范畴上面的态射也可以通过 (fmap :: (Functor t) => (a -> b) -> (t a -> t b)) 来包住: (fmap (plus 1)) :: Functor Int -> Functor Int,要不然你怎么在 Functor 上执行计算?因为 (fmap f fct) 就可以把『盒子』里的东西交给 f 处理然后放回去?从来就没有一个能够『放置』的盒子。
所以你听我说完以后再去看 某图 是不是莫名觉得很正常一样呢。
这张是不是更正常呢? 好吧一点也不
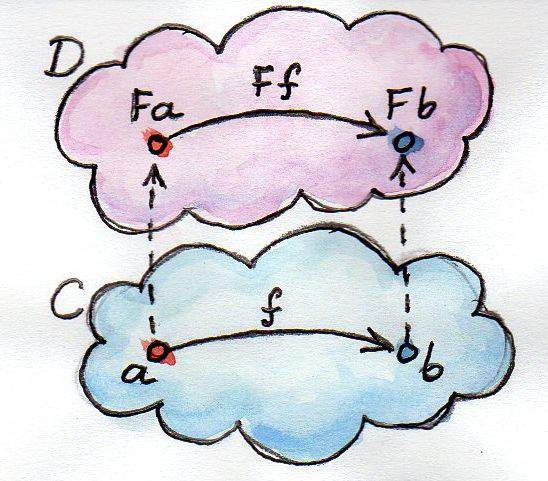
至于它到底有没有包住一个范畴的,其实包住「取值」就是包住范畴了,毕竟我们认为每一个「箭头」都对所有可能的对象产生了映射动作。在 Nat 的例子里,Nat 类型有一个无递归架构器,数据对象 (Z :: Nat),也可能有除了 (S :: Nat -> Nat) 的箭头,可是只要 Functor 包住了某个 Nat,接受它的箭头都会正确映射当前组合修饰出的对象到其他对象,换句话说就是等于包住了整个范畴。
不要以『状态转移』的思路对付Haskell,会很奇怪的。
最后自然就是一些 JavaScript 的『函子』了,这是方便你们学习, 我不是盗的、我不是盗的、我不是盗的。
两种语言是为了尽可能减少思维僵 江 化。
就有一个 Functor,我们认为它什么都不做只是以 f 修饰内部范畴。
function ctorRef(ctor) { return (...cargs) => new ctor(...cargs); }
class Functor {
constructor(x) { this.x = x; }
map(f) { return Functor.of(f(this.x)); }
}
Functor.of = ctorRef(Functor);
Functor.of("em").map(s => s+"mm").map(console.log);
newtype Identity t = { {-key-}runIdentity :: t{-key's type-} }
{- Equiv t (Identity t) -}
Identity :: t -> (Identity t) -- from
runIdentity :: (Identity t) -> t -- to
runIdentity (Identity 1) -- 1
instance Functor (Identity :: * -> *) where
fmap f x = Identity (f (runIdentity x))
{- fmap f (Identity x) = Identity f x -}
instance Monad (Identity :: * -> *) where
return x = Identity x
(x >>= f) = f (runIdentity x)
{- (Identity x >>= f) = f x -}
友情提示:大括号 {--} 里的模式匹配解构版本更好看。
不会?一脸蒙蔽?没关系,多看几遍就好了,幼稚园级别我至少蒙蔽了两周。
因为可以方便地抄代码我就又抄了个 Scala 的版本
不过 Scala 没有 Typeclass,所以要用 implicit val 隐式转化(注意 Scala 里泛型是方括号)。
case class Identity[A](run: A)
Identity(1).run // 1
implicit val identityFunctor: Functor[Identity] = new Functor[Identity] {
def fmap[A, B](f: A => B): Identity[A] => Identity[B]
= { case Identity(x) => Identity(f(x)) }
}
implicit val identityMonad: Monad[Identity] = new Monad[Identity] {
def pure[A](x: A): Id[A] = Identity(x)
def flatMap[A, B](f: A => Identity[B]): Identity[A] => Identity[B]
= { case Identity(x) => f(x) }
}
还有 Maybe,我们认为它就是 Kotlin 的 (x?.let) where x: T? <T: Any>
class Maybe {
constructor(x) { this.x = x; }
static of(x) { return new Maybe(x); }
map(f) { if (this.x ==null) return this;
else return Maybe.of(f(this.x)); }
}
Maybe.None = Maybe.of(null);
const w = _ => console.log('w');
Maybe.None.map(w);
Maybe.of(1).map(w); //w
import Prelude hiding (Maybe, Just, Nothing)
data Maybe t = Just t | Nothing
instance Functor Maybe where
fmap f Nothing = Nothing
fmap f (Just x) = Just (f x) -- apply and "wrap"
main = do
--((\_ -> putStrLn ":/") <$> Nothing)
-- 大家可以看到它是 Maybe IO (), 要 Alternative 很麻烦,算了
case (print . (+1)) <$> (Just 1) of
(Just r) -> r
其中 f <$> fct 就是 fmap 的中缀版本。
trait Maybe[+T]
case class Some[T](x: T) extends Maybe[T]
case object None extends Maybe[Nothing]
implicit val maybeFuctor: Functor[Maybe] = new Functor[Maybe] {
def fmap[A, B](f: A => B): Maybe[A] => Maybe[B] = { // match function
case None => None
case Some(x) => Some(f(x))
}
}
Kotlin 为了有人用,牺牲了 Higher kind(、类型架构器什么的)这种高端操作,没法作为一个父类来定义 Functor 因为 fmap 的返回类型 Fct<R> 依赖输入 f: (T) -> R 确定而依赖在 函数范围的类型变量 R、Functor 只能在类级别收它子类的类型变量 Maybe<T> 或者 Maybe<*>,Kotlin 的泛型又只有 裸类型(raw type)和参数填完了的类型,拿不到 Maybe<R>。 好吧其实没有裸类型,但是有星形投影版
sealed class Maybe<out T> {
data class Some<T>(val item: T): Maybe<T>()
object None: Maybe<Nothing>()
fun <R> fmap(f: (T) -> R): Maybe<R> = when (this) {
is Some -> Some(f(item))
is None -> None
}
}
还有 forall a. Either a,它表示可能是 a 或者 b,不过这里篇幅原因不说。
data Either a b = Left a | Right b
还有 Applicative,它很方便就可以把自己上的 箭头 t (a -> b) 拿来进行自己的范畴上的态射(比如 List (Int -> String))。
class Functor t => Applicative (t :: * -> *) where
pure :: a -> t a
(<*>) :: t (a -> b) -> (t a) -> (t b)
比如,字符串处理(实际上很多时候在Haskell都是列表 [Char] 处理……)
instance (Applicative Maybe) where
pure x = Some x
(<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
(Nothing <*> x) = x
(Just f <*> x) = Just (f x)
之前没写过多少 Haskell,还是复制星野大佬的吧。
(+) <$> (Just 1) <*> (Just 2) == 3
pure (+) <*> (Just 1) <*> (Just 2) == 3
刚才我们谈到了 Functor、Maybe、Applicative,相对于阮老师的版本只是没谈到 Either、Monad、IO,当然或许也谈到了,我觉得剩下的部分还是去看星野大佬的吧。
是类型类!还有函子,可应用函子和单子! by HoshinoTented 2019.10.28
再看看这张图吧
灵魂画师duangsuse手绘早期作品
算了暂时不发,数位板有点冰凉……
本文使用的Haskell教学
为了描述语法,引入 形式化语言
其实要描述Haskell靠你自己 模式识别 就可以了,不过我觉得既然没那么困难还是顺便多学一点好,实在不行可以先看后面的。
a b c表示项 a, b, c 按顺序出现(a|b|c)表示 一项,可能是 a, b, c 之一{a}表示 a 会 出现 并且 可能重复出现a?表示 a 可能出现也 可能不出现a~t表示 直到 t 出现 a 可能重复出现
我们进行序列(sequence)解析(parse)的核心是记住当前在进行 推导 的流(stream)位置,按『顺序、判断、重复』这三个操作去读取它。
时间 "早上"|"上午"|"下午" -- a|b|c
X好 时间 '好' -- a b c
X好 < [早,上,好] => (X好 (时间 "早上") 好)X好 < [上,午,好] => (X好 (时间 "上午") 好)
上面 X好 是一个解析日常打招呼的例子,至于如何推导一般是用递归下降法(recursive descent)自顶向下(top-down)从 入口规则 按部就班地读取或判定,就是你无师自通的方法。不用教了。
多谈一点关于形式化文法的内容
文法推导一般包含两种项定义: 终结符(单项) 和 非终结符(推导过程),这里约定
_,[a-z](小写)开头的名字代表终结符(terminator)- 否则代表非终结符(non terminator)
然后有个 LL(k) 的形式化文法子类 where k in Nat
LL 是 Left(扫描顺序是从左到右)、Lookahead(预取项目数)的简写
_爱 '爱'
心如血滴 "心如血滴"
某歌词 '我' {_爱 '你'} _爱'到' 心如血滴
奇奇怪怪的歌词
上面 某歌词 是解析一句包含重复的歌词 我爱你爱你爱你爱到心如血滴 的例子,这里就不点名了。
写成这样难看是为了让你知道其实不止是那一种写法。
Noun "the"? ("monkey"|"tree"|"baby")
|(Noun Noun) -- green dog feet
|Place|Of
Of Noun "of" Noun
Verb ("act"|"play")'s'? |(Verb Adj)
Adj Place
Place "top"|"over"
Stmt
Noun Verb Noun
比如说,[baby monkey acts over the top of the tree]
(Stmt
(Noun (Noun "baby") "monkey")
(Verb (Verb "act" 's') (Adj . Place "over"))
(Of (Noun "the" Place "top") "of" (Noun "the" "tree")))
糊涂了吧?我都写岔了……
Haskell 词法
[abc]表示 一个字符,可能是'a','b','c'[A-Z]表示 一个字符,可能是'A','B', …,'Z'[A-Za-z]表示 一个字符,可能是'A','B', …,'Z'或'a','b', …,'z'[_A-Za-z]表示 一个字符,可能是'_'或'A','B', …,'Z'或'a','b', …,'z'\n表示 换行符(newline)anychar表示任意字符
whitespace [' '\n]
Comment "{-" anychar ~"-}"
ws {whitespace|Comment}?
Name
[a-zA-Z]{[_a-zA-Z0-9]}?
|[_a-zA-Z]{[_a-zA-Z0-9]}
Number digitNZ|LongNum where
LongNum digitNZ{digit}?
Token = Name|Number|String|ws
算了好累啊,大家直接看下一条好了,当我没写这部分。
使用到的Haskell语法
Haskell 支持很多 pattern matching destruct模式匹配解构 啊,比如
(one, two) = (1, 2) -- tuple
newtype Monkey = Monkey (Int, String)
Monkey m@(id, name) = mky where
mky = Monkey 0 "Hou"
id == 0 && name == "Hou"
-- 还可以有record { x :: t }, { x = (x :: t) }
-- cons (x : y)
-- list [o0, o1]
-- 什么的这里不说了
其中 where 是作用域语法,当然它的含义就是『XX为……』定义,这是个2D文法(缩进带语义的文法)。
two = let one = 1 in one + one
two == one + one where
one = 1
然后这门语言有『lambda』(废话,没有lambda的Haskell还能用吗),还可以『apply』
Lambda '\' formals "->" body -- 准确的说作语法叫Abstraction
Apply Expr Expr | Apply Expr -- 准确的说作语法叫Application
-- Apply Expr 左递归
LambdaRec '\' LexicalScope!"->" -- 不能没有参数直接上body
LexicalScope Name LexicalScope | "->" Expr -- 右递归
Lambda 就是一种在项(term)的形式化系统(formal system)上进行的抽象(abstraction)
前面的 formals形参 是它的参数们,后面的 body体 是『函数体』,当然我们知道 参数叫什么名字都可以的,只要在体里面的引用处都相等 就是了;类似代码重构的重命名操作,这个性质被 Lambda 演算称为『alpha equivalence』。
在我们 展开(reduce) 任何 函数应用(application) 的时候,首先我们要把 体 里对应的 形参 引用全部 替换(subtract) 成实际的 调用的参数(arguments)
这时被实例化的 体 就可以继续展开下去了,它上面被替换的变量被称为 substitution。
递归(recursion) 在 lambda 演算里是被允许的,函数可以通过各种形式引用到自身,当然也有。
y = \f -> let k = \c -> f (c c) in (k k) 应用序Y组合子(applicative order Y combinator) ,当然这是假设Haskell 无类型(untyped) 啦,怎么可能呢。
说到lambda比如,
(\a b -> a+b) 1 1 {- a+b [a:=1, b:=1] -} == 2
还支持 currying柯里化,意思是说
plus = (\a b -> a+b) 1 -- a=1
plus' = (\a -> \b -> a+b) 1 -- a=1
plus 1 == plus' 1
plus 和 plus' 其实是等价的,而且 \a b -> … 本就是简记 \a -> \b -> …
最近的函数式编程语言往往会把 currying 给换成更规范的 partial application,就是说:
def plus(a: Int, b: Int): Int = a+b
val plus1 = plus(1, _: Int)
plus1(1) //2
一般把它称作 Lexical scoping词法作用域,为什么叫这名是因为一般对 formals 与 body 里形参的引用是在 代码序列文法解析 过程的 词法处理 阶段被联系起来的,而且只有在这里才能和 动态时序作用域、静态嵌套序解析作用域 彻底分开,不过这种性质在『部分应用』的时候就构成了 闭包(closure),闭包里被 捕获(capture) 的 父级(outter function)参数被称为 UpValue上值、而整个闭包的词法作用域实例被称为 binding作用域绑定,相应地binding里包含的 变量 被称为 bounded variable绑定变量、binding里没有的则被称为 unbound variable 或者 free variable自由变量。
提供了一个参数的lambda依然是lambda,但它就从 全局单实例 引用变成 新建实例 引用了,因为 a 是变量被包在了闭包里,提供了 体 里 a 的值而不必再传参数。
关于时序作用域和嵌套序作用域的区别有个非常经典的例子:
(define a 'apple)
(defun get-a() a)
(defun main()
(define a 'angle)
(display (get-a))) ; angle
对于任何嵌套序作用域的语言来说,(main) 只会显示 'apple,因为 (get-a) 的行为早在创建它的时候就已经固定为返回 global 的 (define a 'apple) 了。
但是在时序看来,解析是动态、自 栈顶 向下到 全局作用域 的,所以具有相同 identifier标识符,名字 的 define a 就 后来居上 了。
词法作用域则完全可以在词法处理阶段就把 两个 a 的底层存储区分开。在不同的地方,相同的名字也可以指代不同的含义、不一样的存储引用,即便词法作用域最重要的是可以创建『闭包』而不止一个静态区分。
然后还有 data,data 定义一个用户数据,可能有很多 | 分的 构造器(data constructor) 包含很多 字段(field)能够构造一个 类型(data type),一般认为 类型是它所有可能值的集合。
由 | 分割构造器类似 sum type(tagged union)、Constructor A B 并列代表 product type。
sum 和类型意思是 (GreenApple, RedApple) :: (Apple, Apple) 的都能是 Apple,当然在使用 DataKinds 之前他们都只是构造器而不是子类型(subtype) 当然开了也不是,毕竟Haskell是代数数据类型AlgebraicDataTypes,product 积类型代表一堆状态叠加在一起,他们组合的所有可能。
a :: T 读作 “a has type T”, Haskell 里类型名、构造器名都 必须 是大写。
其实 newtype 也是一样的,不过它 exactly one constructor, exactly one field。
data Apple = GreenApple | YellowApple | RedApple
type PingGuo = Apple -- type synonym
data Gender = Male | Female
data Human = Human Gender String | AnonHuman Gender
giveApple :: Human -> Apple
giveApple (AnonHuman gdr)
|gdr == Male = YellowApple
|gdr == Female = GreenApple
giveApple (Human gdr name) = case (gdr, name) of
(Male, "Jack") -> RedApple
(Female, "Rose") -> YellowApple
otherwise -> GreenApple
然后还有 Typeclass类型类,类型类就是定义一些 Hindley-Milner 多态操作符(就是『函数』)的规范,也可以说这些类型类的实例上 共有 这些 操作。
忘记举例了,比如 Haskell 的 Eq, Ord 都是,相等关系 和 全序 的 传递性(transitive)就不用说了。
Prelude> :k Eq
Eq :: * -> Constraint
Prelude> :k Ord
Ord :: * -> Constraint
class Destroyable t where -- Typeclass "Destroyable"
destroy :: t -> t -- polymorphic operator destroy
data Color = R|G|B deriving Enum
inv :: Color -> Color
instance Destroyable Color where
destroy c = inv c -- 也可以直接 Point-free 约掉两边的参数 c 了
这个时候就有点像面向对象的『接口』,不过要手动传『接收者』的类型 t(但是差别还是很大的)。
class, instance 后面也可以跟额外的类型约束 (c, c1, ...) => ,比如某个 Typeclass 的实例 (Destroyable Door) :: Constraint 什么的。
想要了解 Haskell 的类型系统和类型推导算法可以去隔壁 miniKanren 看一下。
这就是 简要 版本的说法了,还有详细一点的:
- A Gentle Introduction to Haskell, Version 98
看完以后我越来越确信我的菜鸡了 - 星野大佬的博客
